
De Oracle Primavera Cloud (OPC) risico module bleek in het verleden nog veel af te wijken van Oracle Primavera Risk Analysis (OPRA), de al jaar en dag betrouwbare risico analyse software. De P50 en P80 data in OPC weken toen 30+ werkdagen af van de data die OPRA genereerde. Nu hebben we opnieuw voor een project de risico analyse vergelijking gemaakt tussen OPC en OPRA en deze analyse rapporteren we hier in detail.
De risico analyses zijn uitgevoerd op alle activiteiten met 5000 iteraties, zonder convergence en met dezelfde random seed (1). Het voorbeeld project waarop de analyses zijn uitgevoerd bevatte meer dan 1000 activiteiten en 125 risico’s die allen zijn meegenomen. Initieel waren er geen onzekerheden toegepast op dit project, later is er ook een analyse met onzekerheden op alle activiteiten uitgevoerd. Deze onzekerheden hadden een minimum van 90%, most likely van 100% en maximum van 130%. Het project dat geanalyseerd is loopt over een periode van 5+ jaar. Er is ook een risicoanalyse op de kosten gedaan, hierbij is gekeken naar wat het effect was van het koppelen van kosten aan verschillende risico’s. Deze kosten waren uniform verdeeld met een minimum van 600k en maximum van 1.2 miljoen. Het project had drie harde constraints met betrekking tot starttijden van drie activiteiten. Er zijn analyses met en zonder deze constraints uitgevoerd. De response context was pre-response, omdat er nog geen actieve mitigatie was uitgevoerd op het project. Er was gekeken naar de finish dates, de P50 en P80 waardes, en de deterministische probability.
De eerste vergelijking van OPC en OPRA laat zien dat voor de finish date van het geteste project de P50 en P80 waardes maar 2-3 werkdagen afweek van elkaar op een P buffer van 180 werkdagen (namelijk het verschil tussen P0 en P50). De deterministische probability was bij zowel OPRA als OPC 5%, wat erop duidt dat OPC nu betrouwbaar is. De frequentie van de finish dates was gelijk voor OPC en OPRA (Figuur 1). Het enige verschil was in de maximum datum die 30 werkdagen afweek tussen OPC en OPRA op een P buffer van 492 werkdagen, waarbij OPRA de datum later plande. Echter is deze maximum datum een outlier in de 5000 iteraties van de analyse, en wordt deze datum bijna nooit gerapporteerd in projecten.
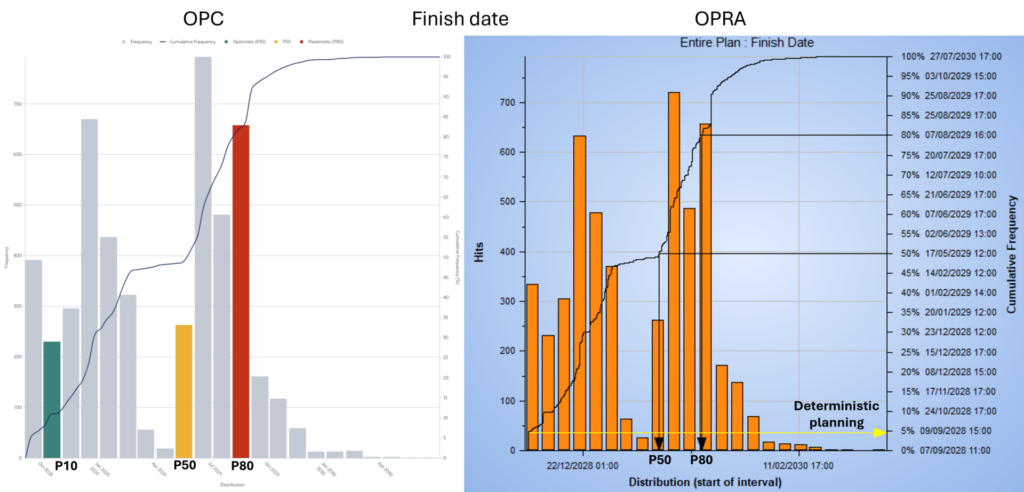
Figuur 1. Vergelijking van de frequentie van de finish dates van het geteste project over 5000 iteraties met daarin P50 en P80 waardes.
Naast de finish date van het algehele project is er ook gekeken hoe de finish dates van tussenmijlpalen verschilden in de risico analyses van beide programma’s. Bij tussenmijlpaal 1 weken de P50 en P80 finish dates maar 1-2 werkdagen op een P buffer van 112 werkdagen af tussen OPRA en OPC, maar bij tussenmijlpaal 2 had de P80 mijlpaal 8 werkdagen afwijking op een P buffer van 152 werkdagen en was de P50 gelijk voor beide analyses. De deterministische probability voor de ene mijlpaal was 5% volgens de OPRA analyse en 5.9% voor OPC, terwijl bij de andere het 22% voor OPRA en 28.6% voor OPC was. De frequentie grafieken van beide tussenmijlpalen laten dezelfde trend zien, net zoals voor de finish date van de algehele planning (Figuur 2). Voor beide mijlpalen was er een afwijking tussen OPRA en OPC op de maximum finish date van 30+ werkdagen (32 en 36 respectievelijk op P buffers van 450 en 405 werkdagen).
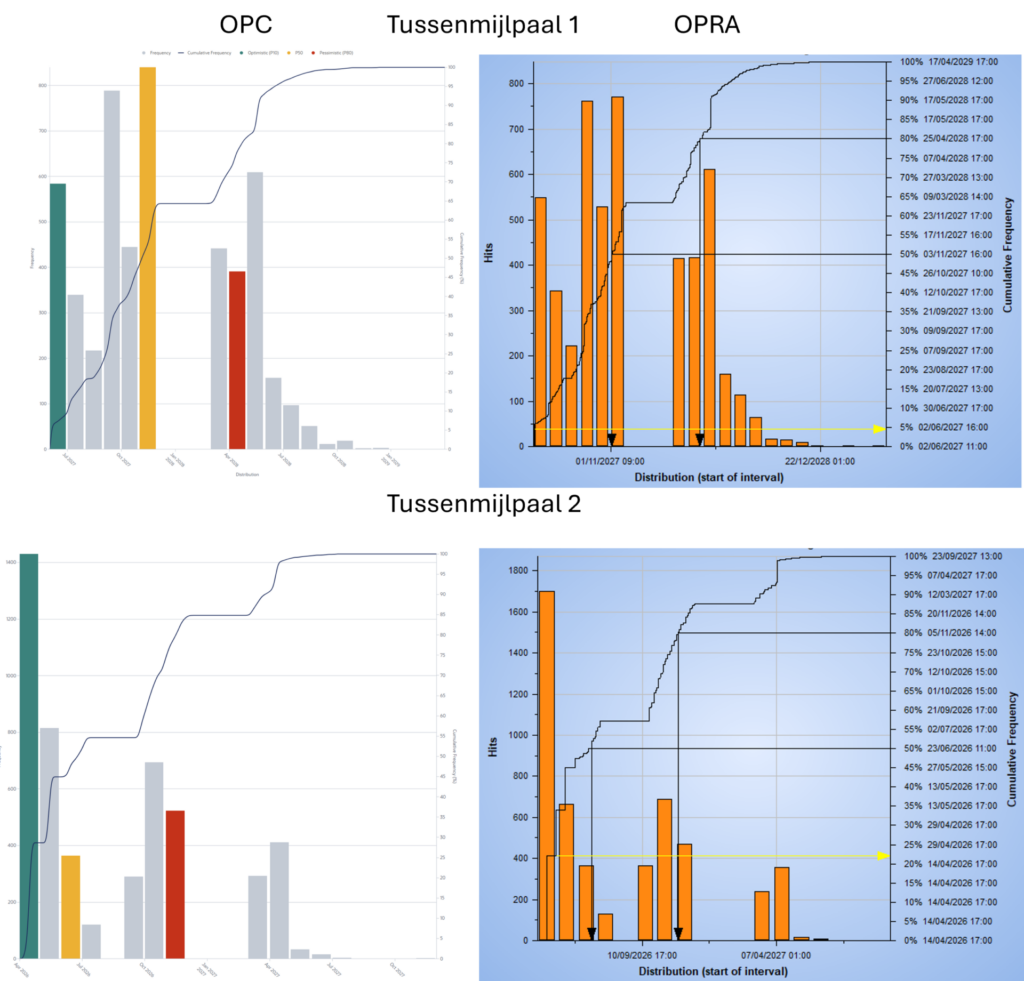
Figuur 2. Vergelijking van de frequentie van de finish dates voor twee tussenmijlpalen van het geteste project over 5000 iteraties met daarin P50 en P80 waardes.
Na wat aanpassingen in de risico’s die volgde uit een progressie update van de planning is de risico analyse nog een keer uitgevoerd, nu met harde constraints op drie activiteiten waardoor deze altijd op de constraint datum startten. De P50 en P80 finish dates waren hetzelfde voor de OPC en OPRA analyse. Ook de mean finish date had maar een afwijking van 1 dag op een verschil van 132 werkdagen tussen mean en P0. In deterministic probability was wel verschil: namelijk 7% volgens OPRA en 9.1% volgens OPC. De maximum finish date had een groot verschil van 86 werkdagen op een P buffer van 480 werkdagen. De frequentie grafiek laat weer een gelijke trend zien tussen OPC en OPRA, maar bij OPC zie je meer hits op de deterministische finish date wat het verschil in deterministic probability verklaart (Figuur 3).
Dezelfde analyse was ook uitgevoerd zonder de constraints; voor de P80 en mean finish dates was het verschil tussen de OPC en OPRA analyses alsnog maar 2-3 werkdagen op 229 werkdagen P buffer. Echter de P50 waardes hadden een verschil van 27 werkdagen op P buffer van 174 werkdagen. De frequentie grafieken waren wel vergelijkbaar, en daaruit valt ook te zien dat door een heel klein frequentie verschil al de datum van de P50 finish date zo kon verschillen tussen de programma’s (Figuur 3). Wel opvallend was dat hier de deterministic probability van de finish date wel nagenoeg gelijk was tussen de OPC en OPRA analyse (5% en 5.4% voor OPRA en OPC respectievelijk).
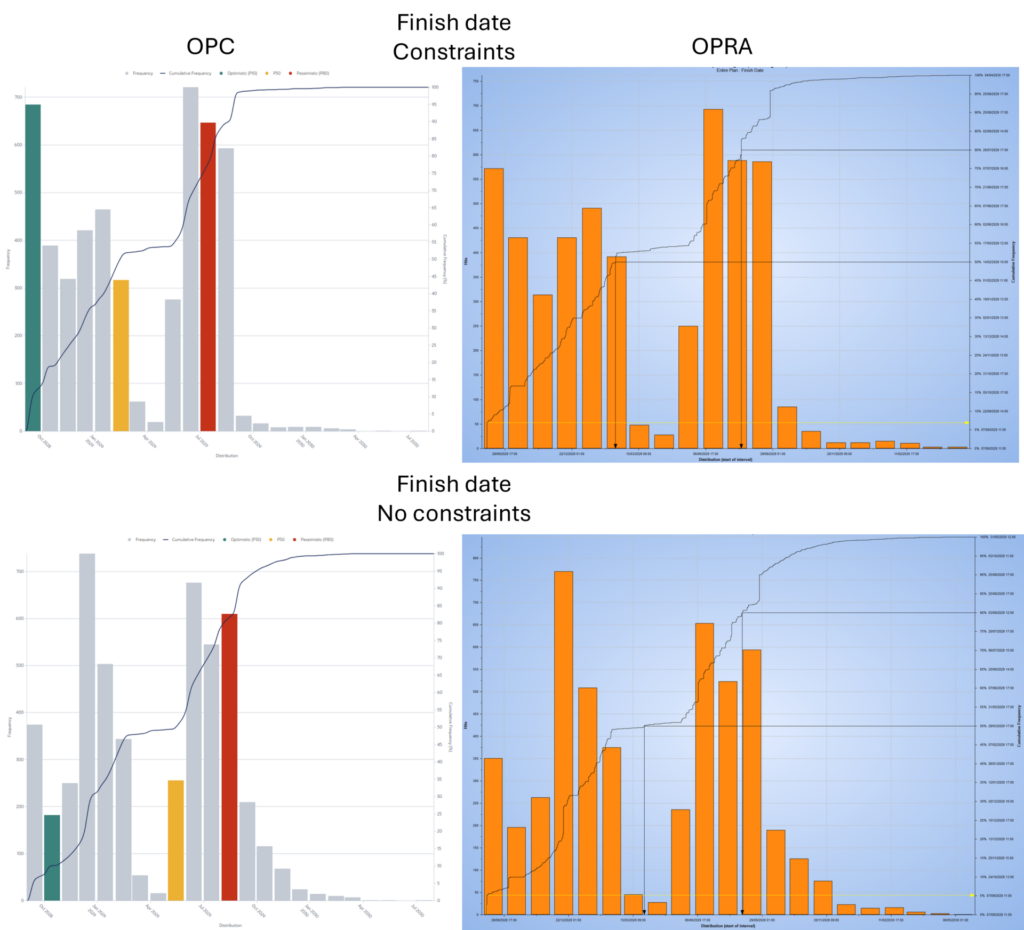
Figuur 3. Vergelijking van de frequentie voor de finish dates van de algehele planning na update met en zonder constraints op 3 activiteiten van het geteste project over 5000 iteraties met daarin P50 en P80 waardes.
Om ook te kijken naar de invloed van onzekerheden hebben we een analyse gemaakt waarbij op alle 1000+ activiteiten een onzekerheid was gezet van minimum 90%, most likely 100% en maximum 130% naast de normale risico’s. Dit is een extreem voorbeeld, maar zo kunnen we het beste vergelijken hoe de OPC risk module reageert ten opzichte van OPRA. Het verschil tussen OPC en OPRA in P50 en P80 waardes voor de finish date was ongeveer 10 werkdagen op P buffer van 224 werkdagen. Dit was iets meer dan in de eerdere voorbeelden, maar nog steeds binnen de marges dat het acceptabel is. In deze vergelijking week ook de minimum finish date ongeveer 10 werkdagen af tussen de OPC en OPRA analyses. (Deze minimum finish date was in alle eerdere analyses altijd gelijk bij beide vergelijkingen, omdat risico’s alleen uitloop konden geven maar onzekerheden kunnen ook inloop geven.) De deterministische probability was heel laag zoals verwacht met zoveel onzekerheden, waar OPRA alleen <1% rapporteerde, was OPC wel in staat om een nauwkeuriger getal (0.02%) te berekenen.
8 risico’s, die ieder betrekking hebben op één activiteit, hebben we aan kosten gekoppeld, dit resulteerde in een deterministische probability (nota: deterministische waarde is geen kosten) van 41% met de risicoanalyse in OPRA en 39.1% voor OPC. Ook de P50 waardes die 7.14 ∙ 105 en 7.41 ∙ 105 waren voor OPRA en OPC respectievelijk, weken maar enkele percentage punten van elkaar af (3.6%). De P80 waardes lagen nog dichterbij elkaar met 1.07 ∙ 106 voor OPRA en 1.08 ∙ 106 voor OPC. De gehele distributie van de totale kosten is nagenoeg gelijk in de OPC en OPRA analyses (Figuur 4).
Waar we ook achter kwamen door deze analyses was dat in OPC de kosten gekoppeld zijn aan het risico, maar bij OPRA aan de activiteit binnen het risico. Dus als het risico optreedt dan worden er eenmalig kosten aan verbonden in OPC. Als het risico optreed en er hangen 5 activiteiten aan deze activiteit dan wordt er in OPRA 5 keer kosten berekend. Dus bij risico’s waar meerdere activiteiten aanhangen, is het goed om te realiseren dat OPC en OPRA anders rekenen.
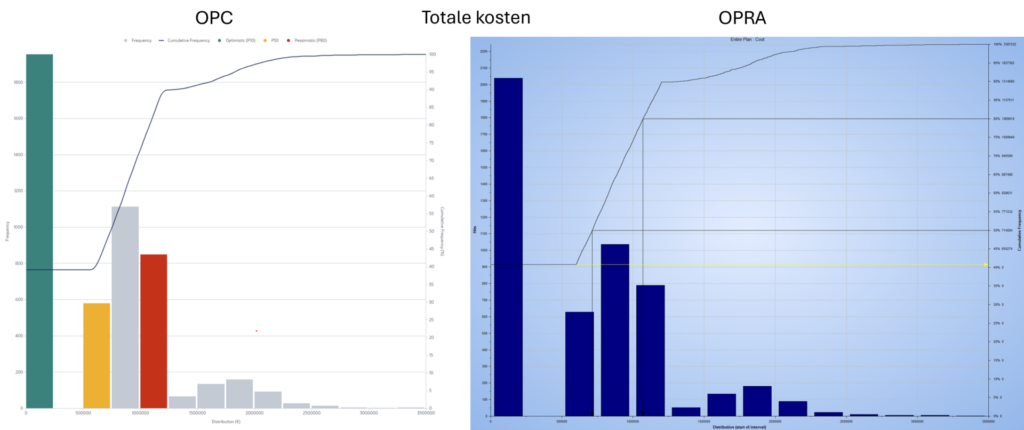
Figuur 4. Vergelijking van de totale kosten van het geteste project over 5000 iteraties met daarin P50 en P80 waardes. Er zijn 8 risico’s met kosten gebruikt voor deze analyse.
Naast de standaard analyse op finish dates en het bepalen van P-waardes, wordt er vaak met risico analyses gekeken naar welke activiteiten en/of risico’s nu het meeste impact hebben op de planning. In OPRA wordt hiervoor gekeken naar zogeheten tornado grafieken. Een voorbeeld hiervan is duration sensitivity, wat inhoudt hoe groot de kans is dat de duratie van een activiteit de algehele finish date van het project beïnvloedt (Figuur 5). Ook is criticality index hierbij relevant, wat weergeeft hoeveel percent van de iteraties een activiteit op het kritieke pad van het project ligt.
In OPC heet deze functie mean impact en laat het zien hoeveel dagen een activiteit en/of risico gemiddeld het project laat uitlopen. In de top 10 van de mean impact (OPC) en duration sensitivity (OPRA) analyses komen nagenoeg dezelfde activiteiten voor (Figuur 5). De enige activiteit die niet voorkomt in de mean impact is 3, en deze activiteit is degene die een constraint op zich heeft vanuit de planning, wat kan verklaren waarom OPC deze niet laat zien in de mean impact analyse.
Deze tornado grafieken laten zien dat OPC een goede inschatting maakt van de mean impact van activiteiten. Het programma heeft alleen een andere manier van het weergeven van de impact van activiteiten en/of risico’s ten opzichte van OPRA.
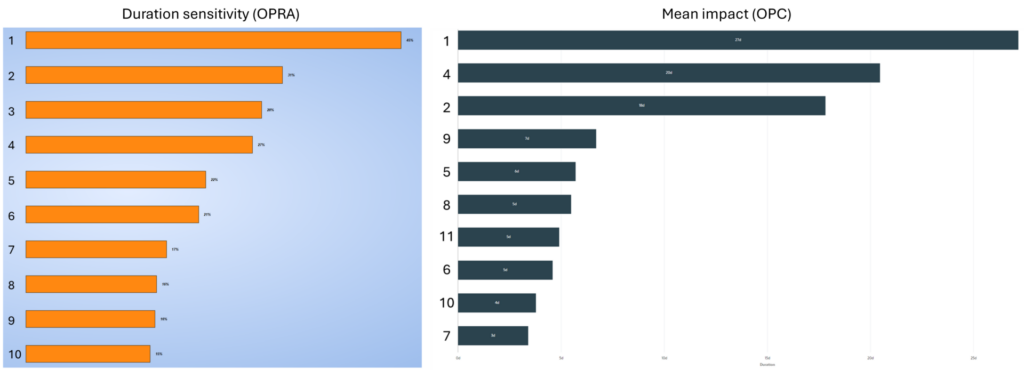
Figuur 5. Tornado grafieken van de risico analyse van de algehele planning na update met constraints die de duration sensitivity uit OPRA en de mean impact uit OPC laten zien.
De OPC-risicoanalysemodule is nu betrouwbaar genoeg om OPRA te vervangen als de standaard voor risicoanalyses, zelfs bij grootschalige en complexe projecten. Deze module is gebruiksvriendelijker dan de OPRA-software en de planning is al geïntegreerd in OPC dus deze hoeft niet langer apart geëxporteerd te worden voor de risicoanalyse. Daarnaast heeft OPC weather risks al geïntegreerd in zijn risicoanalysemodule en zal het platform zich blijven ontwikkelen door meer functionaliteiten voor risicoanalyse toe te voegen.
Een van de andere belangrijkste voordelen van OPC ten opzichte van OPRA is de nieuwe functionaliteit “risk removal impact“. In OPRA moet dit proces handmatig worden uitgevoerd, wat tijdsintensief is. Met OPC kan deze functie echter nauwkeurig de impact van individuele risico’s op de planning meten in vergelijking met andere risico’s binnen het project.
Toch betekent dit niet dat OPRA voorgoed in de ijskast kan. De software biedt namelijk nog steeds geavanceerde risicoanalysefunctionaliteiten die OPC momenteel (nog) niet kan uitvoeren. De twee belangrijkste hiervan zijn probability branching en criticality index.
Meer over dit onderwerp weten?